به حداقل رساندن هزینه انرژی در فولادسازی به روش کوره قوس الکتریکی توسط طرحهای کنترل بهینه
چکیده:
هزینه تولید در صنعت فولاد یک مسئله چالش برانگیز و بهینهسازی انرژی یک بخش مهم است. این مقاله یک طرح کنترلی بهینه را با هدف به حداقل رساندن هزینه تولید فولاد در کوره قوس الکتریکی پیشنهاد میکند.
به طور خاص، نشان داده شده است که تولید به روش کوره قوس الکتریکی، هزینه تولید که یک مسئله برنامه ریزی خطی است را میتوان با ابزارهای طراحی کنترل تنظیم درجه دوم خطی حل کرد که نه تنها یک راه حل بهینه ارائه می دهد، بلکه در یک فرم بازخوردی نیز قرار دارد.
مدلسازی و طرحهای کنترلی توسط سازمانهای دادههای تولید واقعی تأیید میشوند.
- مقدمه:
در صنایع فولادسازی به روش کوره قوس الکتریکی (EAF) با ذوب و تغییر ساختار شیمیایی قراضههای قابل بازیافت، میتوان محصول با گریدهای مختلف تولید کرد. بدیهی است که صنعت فولاد یکی از بزرگترین بخشهای مصرف کننده انرژی است و تقاضای زیادی برای کاهش استفاده از برق و سایر اشکال انرژی در فولادسازی EAF وجود دارد.
به طور کلی، کنترل فرآیند ذوب فعلی به دستی و هزینه تولید بهینه نیست. صنایع فولاد به طور جزیی اتوماسیون اسمی برای EAF دارند اما عمدتاً این پروسه توسط اپراتور هدایت میشود. اگرچه بینش و تسلط اپراتور برای چنین صنایعی بسیار ارزشمند است، اما با توجه به اینکه این بینش بر دستورالعملهای سابق استوار است و نمیتوان تمام عدم قطعیتهای احتمالی را در نظر گرفت روند دشوار میشود، مگر اینکه برای این موضوع یک چارچوب ریاضی توسعه داده شود و یا سیستم و فرآیند اتوماسیون برای آن وجود داشته باشد.
سوابق شاهد هدرفت بخش قابل توجهی انرژی در فرآیند ذوب قراضه میباشد و این به معنای وجود یک فرصت فوقالعاده برای کنترل فرآیند میباشد. خلاف مقالات موجود در این زمینه، این تحقیق مربوط به هزینه تولید و دستیابی به بهینهترین حالت مصرف انرژی جهت ذوب قراضه میباشد. بنابراین هدف مدل موجود در این مقاله با بخش بزرگ مقالات موجود میباشد.
به عنوان مثال، در رفرنس شماره 1، فرآیند کنترلی قابل پیشبینی بر اساس یک مدل تطبیقی جهت دنبال کردن مسیرهای از پیش تعیین شده پیشنهاد شد. نحوه طراحی مسیرهای از پیش تعیین شده مورد بحث قرار نگرفت. در رفرنس شماره 2 یک کنترلکننده PID جهت ثابت نگهداشتن مصرف برق توسط الکترود ها پیشنهاد شد.
در رفرنس شماره 3، یک مدل ایجاد شد، اما هیچ بحثی در مورد چگونگی کنترل آن وجود نداشت. در رفرنس شماره 4، مدلی برای دستیابی به حداکثر توان ورودی به فرآیند ذوب پیشنهاد شد. در تمام این مقالات مصرف کنترلی بهینه جز دغدغهها نبود. در فعالیت حال حاضر، یک مدل ریاضی برای EAF توسعه یافته و پارامترهای ناشناخته آن تخمین زده میشوند. هدف این مدل طراحی یک الگوریتم کنترلی است که مصرف انرژی را به حداقل برساند.
در [6]، مدلی برای دستیابی به حداکثر توان ورودی به فرآیند ذوب پیشنهاد شد. در تمام این کارها، به حداقل رساندن مصرف کنترلی جز نگرانی ها نبوده ولی در کار گزارش شده در اینجا، یک مدل ریاضی از EAF ها توسعهیافته و پارامترهای ناشناخته آن تخمین زده میشوند. هدف این مدل طراحی یک الگوریتم کنترلی است که مصرف انرژی را به حداقل برساند. مدل اتخاذ شده در این مقاله یک سیستم خطی زمان ثابت است که به نظر میرسد رضایت بخش عمل میکند. مهمتر از آن، در مرحله دوم، ورودیهای کنترل بهینه با هدف به حداقل رساندن هزینه تولید محاسبه میشود. از آنجایی که هزینه تولید واقعی در مصرف انرژی و الکترود گرافیتی خطی است، بهینهسازی یک مشکل برنامهریزی خطی است. مشکل برنامهنویسی خطی ارائهدادن طراحی ورودی لوپ باز میباشد اگر چه در نبود یک مدل مبهم و خطای اندازهگیری، این مدل بهینه است اما عملکرد آن در واقعیت تحت این فاکتورها قابل گارانتی نیست.
بخشی از مقاله نشان میدهد که مشکل برنامهریزی خطی برای ساختار خاص EAF میتواند توسط معادله درجه دوم خطی معروف (LQR) حل شود و این راه حل در فرمهای بازخوردبسیار قویتر از راه حل لوپ باز عمل کرده است. تمام مجموعه دادههای استفاده شده در این مطالعه جهت مدلسازی و صحت روش کنترلی، دادههای واقعی هستند که از تاسیسات آسیاب Gerdau Ameristeel در ویلتون آیوا جمعآوری گردیده است. همانطور که در شکل 1 نشان داده شده است این تجهیزات ترکیبی از تاسیسات خردایش قراضه، یک کوره قوس الکتریکی، چند سیستم ریختهگری پیوسته و یک ماشین غلتکدار میباشد.

تصویر شماره یک)
به دلیل شرایط خاص، هیچ مقدار داده واقعی در مقاله نشان داده نشده است، اما نتایج مدلسازی و بهبود عملکرد نهایی نشان داده شده است.
در این قسمت مدل سیستم و هدف کنترل بهینه را شرح میدهیم. واضح است که مدلهای EAF میتوانند برای اهداف مختلف متفاوت باشند. هدف ما بهینهسازی هزینه تولید در عین حفظ کیفیت و کارایی است. بدین منظور، ما بر روی 7 متغیر کلیدی تمرکز میکنیم که توصیف نسبتاً معقولی از دینامیک یک EAF ارائه میدهد:
(i) kilowatt-hour consumption (KWH),
(ii) electrode consumption (?2ℎ),
(iii) percentage of scrap melted (PM),
(iv) average arc current (?avg),
(v) oxygen input (O2),
(vi) gas input (Gas),
(vii) carbon input (Car)
تمام 7 متغیر در زمان واقعی قابل اندازهگیری یا محاسبه هستند. در بین این متغیرها، مصرف کیلووات ساعت (KWH) مصرف انرژی الکتریکی است که بخش قابل توجهی از انرژی کل را تشکیل میدهد. مصرف الکترود (?2ℎ) منظور مصرف الکترود گرافیتی است که به طور قابل توجهی به هزینه کمک میکند، درصد قراضه ذوب شده (PM) نیز درصدی از قراضه میباشد که در فرآیند ذوب و کیفیت آن محدودیت اعمال میکند. در پایان هر فرآیند ذوب، PM باید 100 (%) باشد.
4 متغیر دیگر به ترتیب ورودی انرژی الکتریکی متوسط (?avg) و ورودی انرژی شیمیایی O2 (اکسیژن)، گاز و کربن هستند. تمام 4 ورودی انرژی، به هزینه کلی کمک میکنند و در میان آنها انرژی الکتریکی متوسط گرانترین ورودی است.
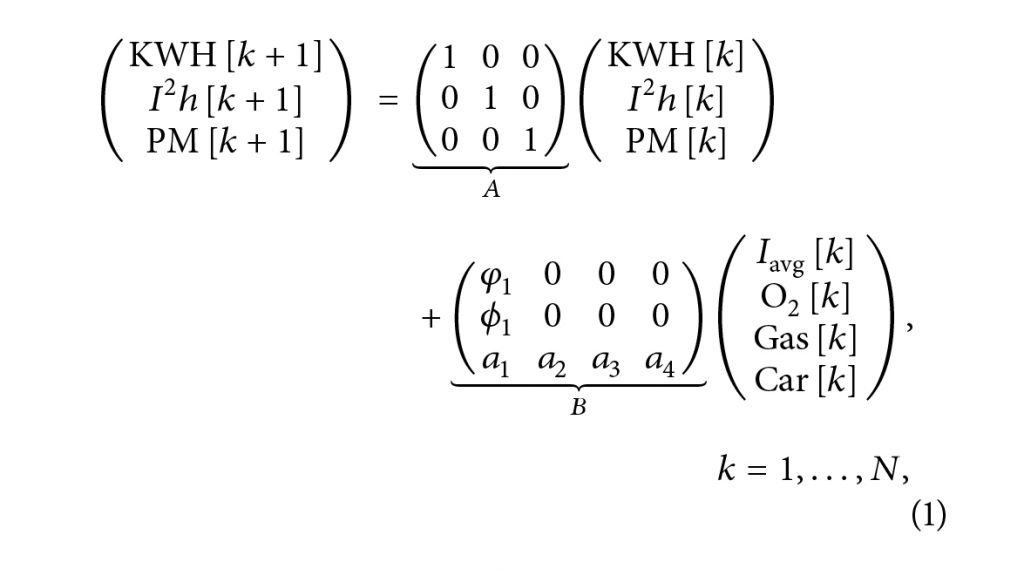
Journal of Energy
بر اساس قوانین فیزیک، افزایش مصرف کیلو وات ساعت (KWH) و مصرف الکترود (?2ℎ) از زمان ??? تا (? + 1)? )??) مستقیماً با ?avg جاری در بازه (???, (? + 1)?? ) مرتبط هستند. از طرف دیگر درصد قراضه ذوب شده (PM)، مربوط به تمام انرژی ورودی در یک دوره مشابه از جمله انرژی الکتریکی و همچنین انرژی شیمیایی است. EAF ساختار زیر را در نظر میگیرد:
که =0 , ?= ??? (??= 5 sec) و ??فاصله نمونه برداری (? + 1)?? کل زمانی است که 100% قراضه باید ذوب شود. این مدل عجیب نبوده و در مقالات مختلف استفاده گردیده است. برای حفظ بهرهوری و کارایی یکسان، (? + 1)? طول کل زمان فرآیند ذوب است و توسط روش فعلی بدون کنترل بهینه از پیش تعیین شده است. ? ماتریسی است که ورودیهای آن به یک EAF خاص و بارهای قراضه بستگی دارد. توجه داشته باشید که ?avg[?], O2[?], Gas[?], Car[?] مجموع انرژی تحویل داده شده به EAF در طول دوره
???, (? + 1)?? ) و KWH[?] و I2h[k] به ترتیب کل انرژی الکتریکی و مصرف الکترود در پایان دوره نمونهبرداری Kth هستند.
| نت | |
هزینه تولید به صورت زیر تعریف شده است:
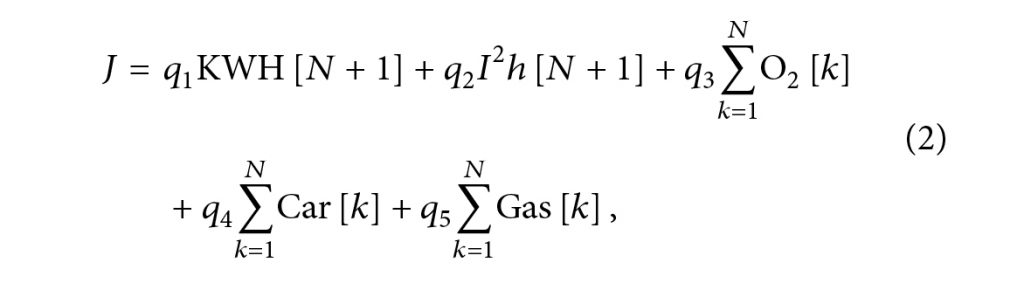
Journal of Energy
که q1,q2, q3, q4 و q5 به ترتیب هزینه هر واحد انرژی الکتریکی، مصرف الکترود و انرژی شیمیایی اکسیژن، گاز و کربن است. هزینه واحد هر ?? با توجه به ارزش بازار در نوسان است و با تغییر قیمت بازار تعدیل میشود. هدف از کنترل، طراحی یک دنباله یا دنباله ورودی
?avg[?], O2[?], Gas[?], Car[?], ? = 1, 2, . . . , ? است به طوری که هزینه تابع (2) را تحت محدودیت زیر به حداقل برساند:
PM(? + 1) = 100. (3)
علاوه بر این، به دلیل محدودیت های سخت افزاری، انرژی ورودی باید برای هر ? = 1, 2, . . . , ?به صورت زیر باشد.
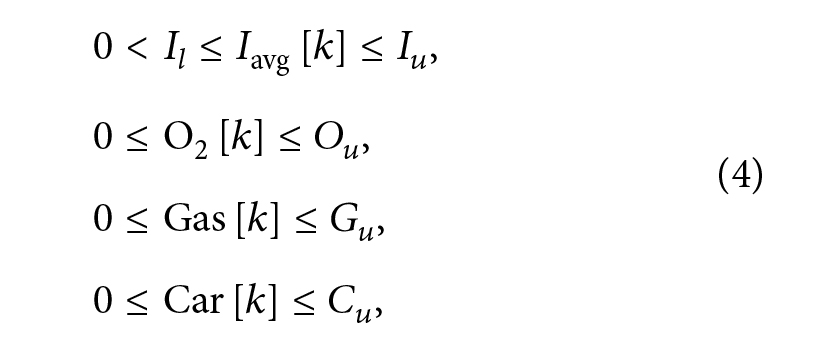
Journal of Energy
اینجا II, Iu, Ou, Gu و Cu حد و مرزهای فیزیکی مقدار انرژی الکتریکی و شیمیایی را که میتوان در طول هر بازه نمونهبرداری ?? به EAF تحویل داد را نشان میدهد.
3- محاسبه کنترل بهینه
برای ساده کردن نمادگذاری، در بقیه مقاله، اجازه می دهیم که:
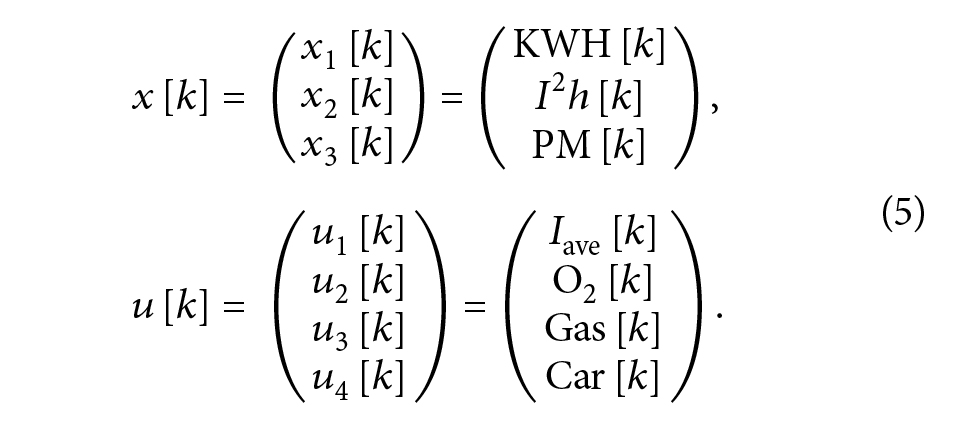
شکل5) محاسبه کنترل بهینه
بنابراین با ساده سازی معادلات متوجه می شویم که:
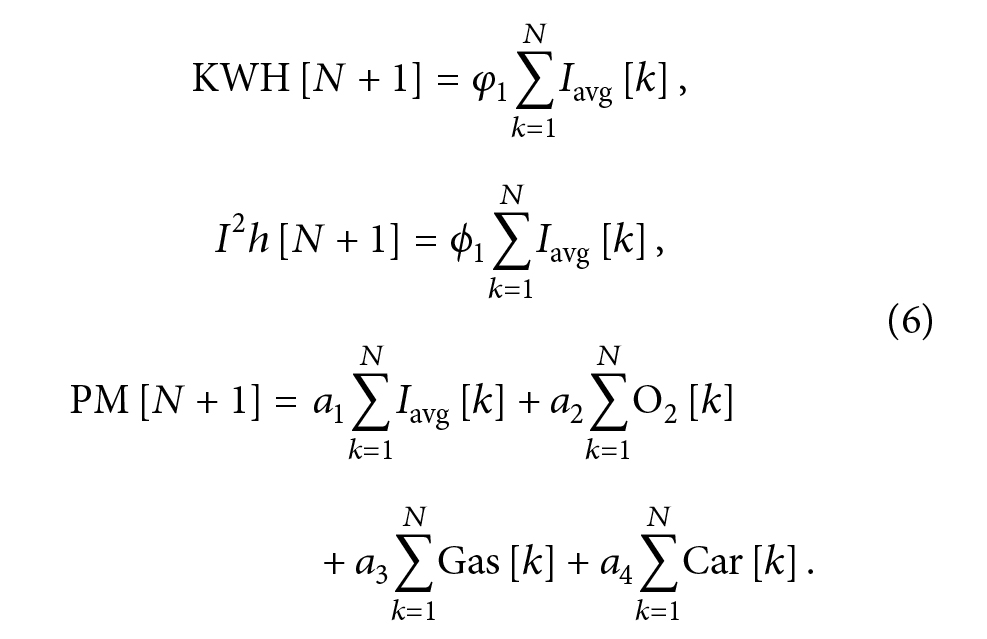
شکل 6) ساده سازی معادله
بنابراین، تابع هزینه (2) را می توان به صورت زیر بازنویسی کرد:
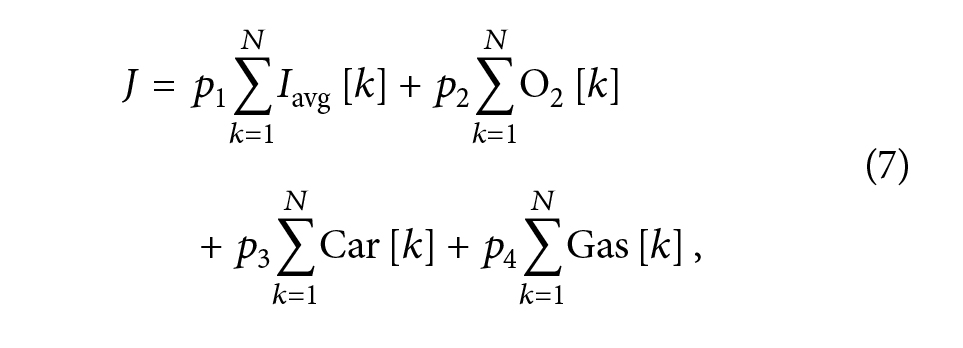
تابع هزینه
که p4=q5 و ?1= ?1?1+ ?2?1, ?2= ?3, ?3= ?4
به طور خلاصه، هدف طراحی یک دنباله ورودی برای یک ui[K] که i=1,2,3,4 و K=1,2,…..,N برای یک N معین به طوریکه تابع هزینه به صورت:
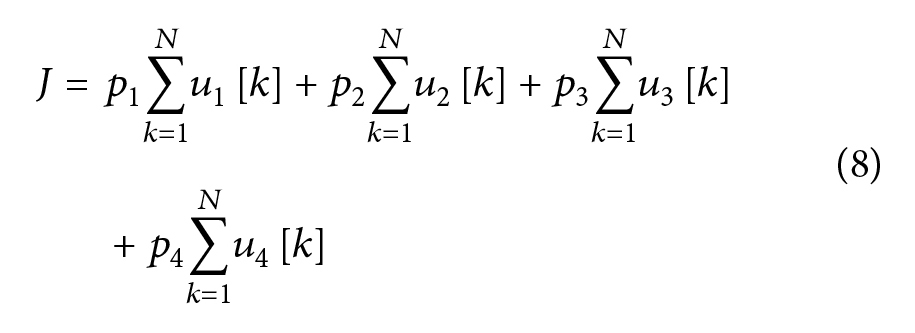
دنباله ورودی
تحت قیدهای برابر و نابرابر به حداقل میرسد،
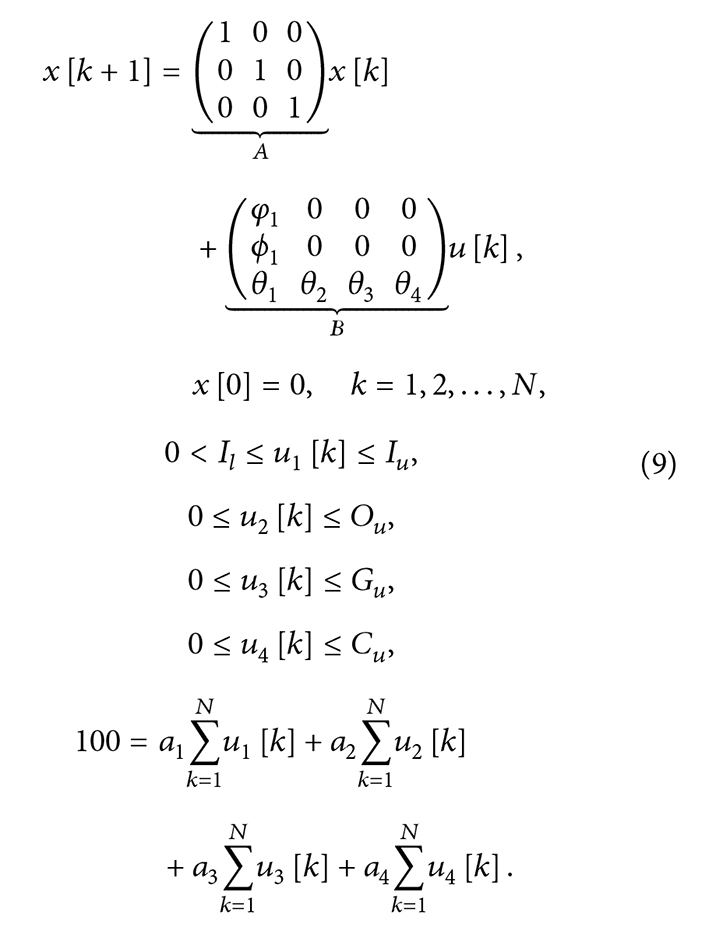
قیدهای برابر و نابرابر
در اینجا، KWH، ?2ℎ، و PM فضای حالت 3 بعدی و ?avg، O2، Car و Gas فضای ورودی 4 بعدی را توصیف میکنند. ماتریسهای ? و ? مانند قبل داده شدهاند.
3.1 راه حل با استفاده از برنامهریزی خطی
مسئله طرح کنترلی بهینه که در بالا توضیح داده شد دقیقاً یک مسئله برنامهریزی خطی با تابع هدف خطی و قیود برابر و نابرابر خطی است. این را میتوان با بستههای نرمافزاری موجود در بازار حل کرد.
برای کاربردهای آنی، پیچیدگی محاسباتی آن یک مشکل است. در واقع، ? تقریباً 1200 است که به این معنی است که 3600=1200*3 متغیر حالت، 4800=1200*4 متغیر ورودی، 9600=1200*4*2 قید نابرابر و 3600=1200*3 قید برابر وجود دارد. به زبان ساده، این یک مشکل برنامهریزی خطی با 8400 متغیر و 14400 قید است. هر بار که مدل تجربی تغییر میکند، برنامهریزی خطی باید دوباره محاسبه شود. توان محاسباتی مورد نیاز برای یک برنامه آنی مطلوب نیست. مشکل دوم این است که برنامهریزی خطی یک کنترل لوپ باز را فراهم میکند. بله، راه حل ?∗[?], K=1,2,…..,N برنامهریزی خطی زمانی که چیز ایده آل باشد حالت بهینه را دارد.
در واقعیت، عدم قطعیت مدل و خطای اندازهگیری همیشه وجود دارد و راه حل برنامهریزی خطی، حلقه باز است. تضمین عملکرد خوب یک سیستم کنترل لوپ باز در حضور عدم قطعیت و خطا، غیرممکن است. آنچه ما ترجیح میدهیم راه حلی است که تابع هزینه (8) را تحت قیدها (9) اما به شکل لوپ بسته به حداقل میرساند. برای این منظور، توجه داشته باشید که طرح کنترلی درجه دوم خطی (LQR) به طور گسترده در مقالات بررسی شده است. راه حل LQR طرحی بازخوردی است که از راه حل لوپ باز ارائه شده توسط برنامهریزی خطی قویتر است. علاوه بر این، کنترل LQR دارای خواص مطلوب بسیاری است.
در بخش بعدی نشان خواهیم داد که با انتخاب مناسب وزنها در محاسبات LQR، راه حل LQR مشکلات برنامهریزی خطی یا به طور معادل تابع هزینه (8) را تحت قیدهای (9) اما به شکل لوپ بسته را حل میکند. اگرچه راه حل برنامهریزی خطی به دلیل ماهیت لوپ باز آن ممکن است عملاً مفید نباشد، برخی موارد مهم را آشکار میکند. اجازه دهید:
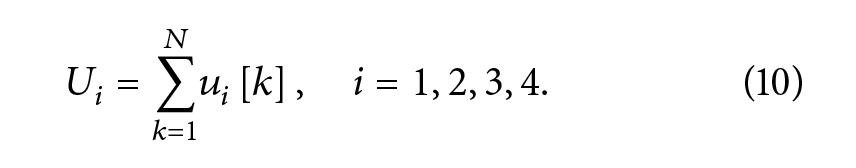
Journal of Energy
سپس، تابع هزینه و قیدهای نهایی را میتوان به ترتیب بازنویسی کرد:
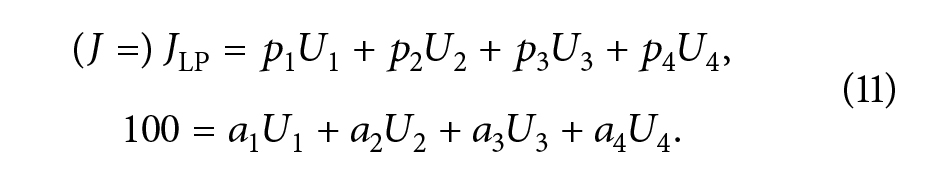
Journal of Energy
همچنین از معادله فضای حالت داریم که ?1 [?+1] = ?1?1 و همچنین ?2 [?+1] = ??1
حالا فرض کنید ?i*[?]’s, ? = 1, 2, . . . , ?, ? = 1, 2, 3, 4راه حل برنامهریزی خطی هستند.
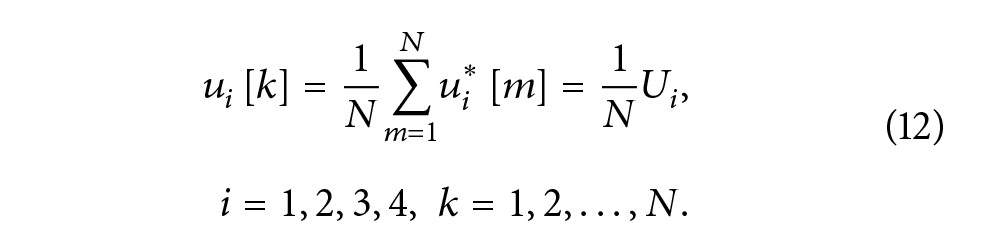
Journal of Energy
واضح است که
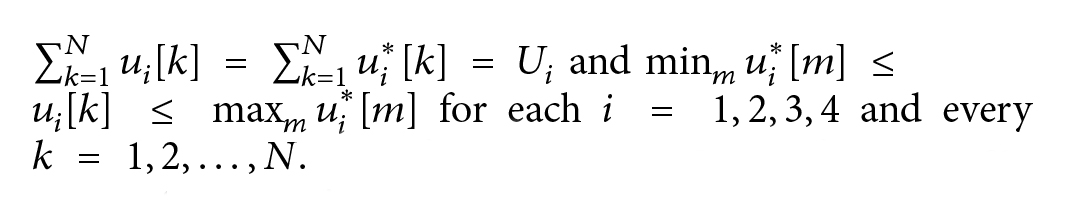
Journal of Energy
بنابراین، راهحلهای ?i*[?]’s های (12) ثابتهایی هستند که تابع هزینه (8) را به حداقل میرسانند و تمام قیدهای برابر و نابرابر (9) را برآورده میکنند. به طور خلاصه، راه حل برنامهریزی خطی ممکن است منحصر به فرد نباشد، اما همیشه به عنوان یک راه حل ثابت وجود دارند. ما این مشاهدات را به صورت قاعده خلاصه میکنیم که بعداً مورد استفاده قرار خواهد گرفت.
قاعده 1: مشکل کنترل بهینه (8) را تحت قیود (9) در نظر بگیرید. سپس، همیشه دنباله های ثابت
?i[?] ≡ ?i[m] ’s , ? = 1, 2, 3, 4 1 ≤ ?,? ≤ ?
وجود دارد که مشکل را حل می کند.
3.2 طرح LQR
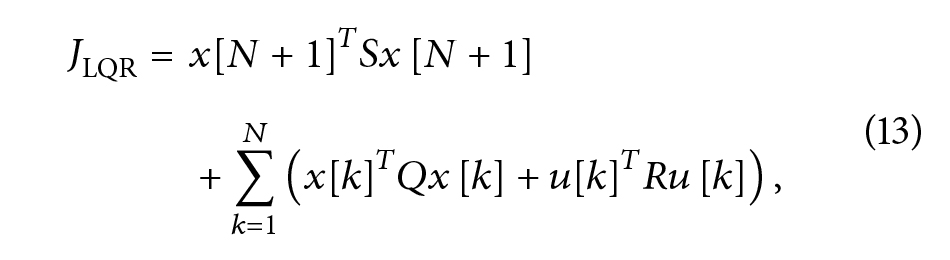
Journal of Energy
که
? = ??≥ 0, ? = ??≥ 0, and ? = ?? > 0
به ترتیب ماتریس هزینههای حالت نهایی،حالت و ورودی هستند. هدف ما در این بخش این است که نشان دهیم با برخی از ماتریسهای ?، ? و ? که به درستی انتخاب شدهاند، راهحل LQR مشکل برنامهریزی خطی را که هدف طرح کنترلی است را نیز حل میکند.
تاکید میشود که LQR نه تنها قویتر است بلکه از نظر عددی نیز کارآمد است. توجه داشته باشید که LQR بازگشتی است و در هر زمان ??، فقط یک معادله ریکاتی (Riccati) با بعد ثابت (در مورد ما، 4 بعدی) باید محاسبه شود [7، 8].
برای این منظور تنظیم کردیم که:
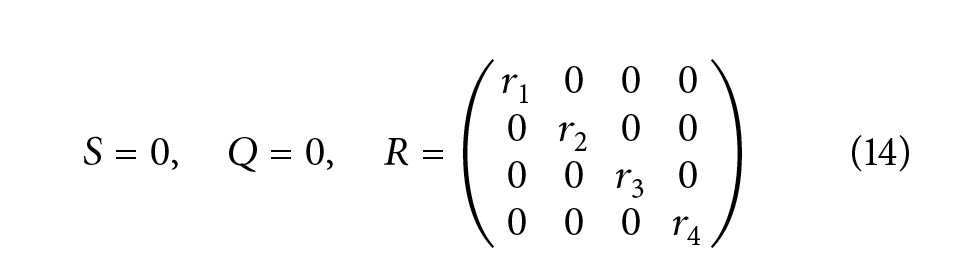
Journal of Energy
برای برخی ri > 0 یا معادل آن
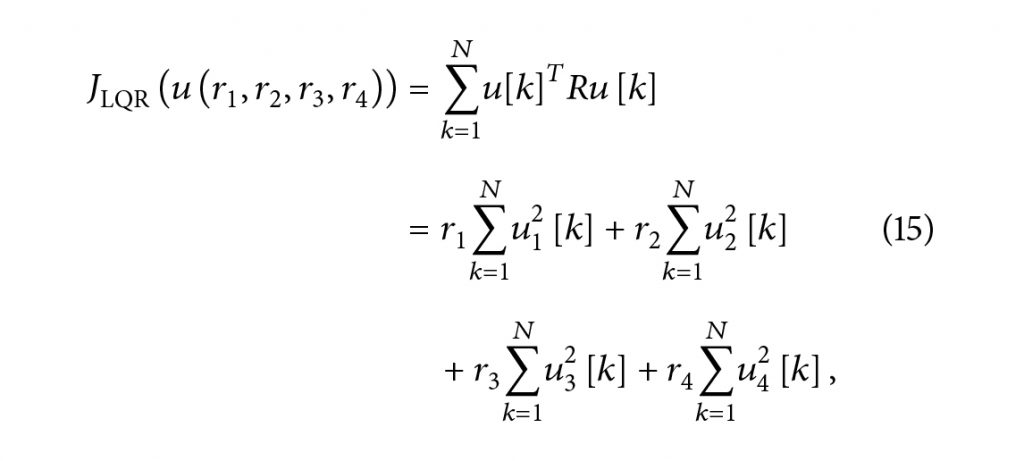
که در آن ?LQR(?(?1, ?2, ?3, ?4))ن شان میدهد که هزینه به دنباله ورودی بهینه ?[?] بستگی دارد که به نوبه خود به وزنهای ri’s بستگی دارد. همراه با محدودیت نهایی در (9)، راه حل LQR شکل [7، 8] را به خود میگیرد.
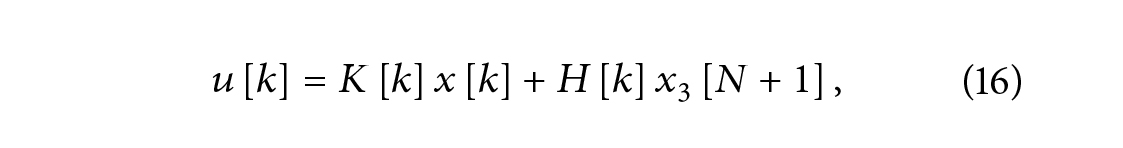
Journal of Energy
که K[.] و H[.] توابعی از ?1, ?2, ?3, ?4 هستند. توجه داشته باشید که دنباله کنترلی فرم بازخوردی است. خوانندگان علاقه مند ممکن است جزئیات بیشتری را در بسیاری از کتابهای درسی بیابند، به عنوان مثال، [7، 8].
قاعده 2: مشکل LQR (15) تحت قیدهای (9) را در نظر بگیرید.. سپس دنباله ورودی
?i*[?]’s, ? = 1, 2, . . . , ?, ? = 1, 2, 3, 4
که مشکل LQR را حل می کند باید دنباله ثابت زیر
?i[?] ≡ ?i[m] ’s
برای تمامی
? = 1, 2, 3, 4 1 ≤ ?,? ≤ ?
باشد.
اثبات: اثبات توسط تناقض
فرض کنید حداقل یک k وجود ندارد، بنابراین برای برخی i ها رابطه زیر برقرار است:
?i[?] ≠ ?i[k+1]
اجازه دهید که
?i*[m] ’s , ? = 1, 2, 3, 4 , m = 1, 2, . . . , ?
دنباله دقیق ui*[m] به جز در K و K+1 باشد.
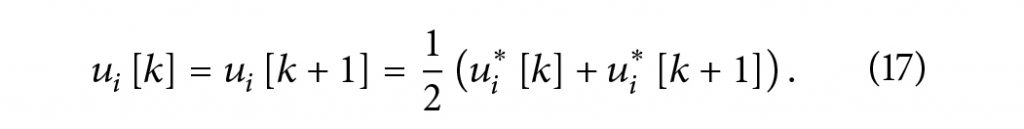
Journal of Energy
بنایراین
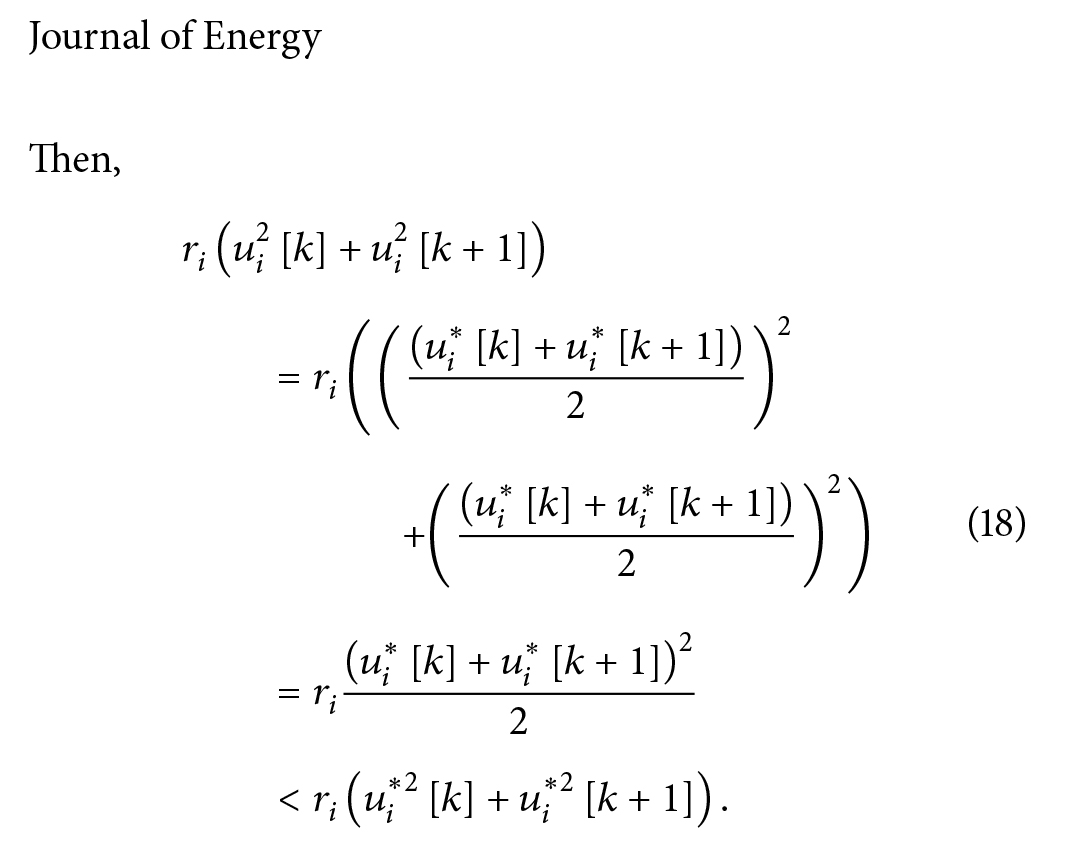
Journal of Energy
به عبارت دیگر، تمام محدودیتهای (9) توسط دنبالههای جدید ??[?] برآورده میشوند، اما تابع هزینه تولید شده توسط ??[?] به شدت کوچکتر از تابع هزینه تولید شده توسط ??*[?] است. دنبالهها ین اثبات را به پایان میرساند. اکنون اجازه دهید دنباله راه حل مشکل LQR (15) تحت قیود (9) نشان داده شود:
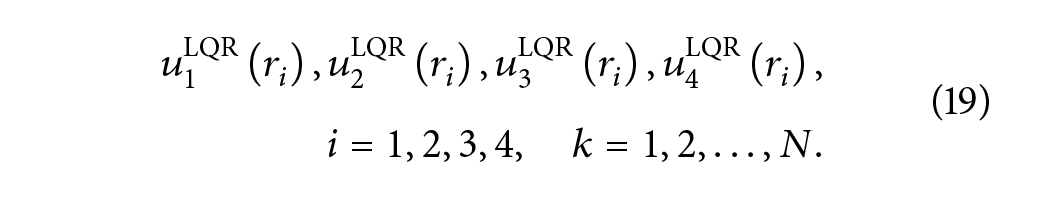
Journal of Energy
علاوه بر این اجازه دهید:
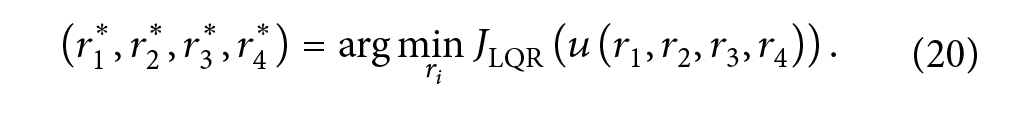
Journal of Energy
حال ادعای زیر را داریم:
قاعده 3:
راه حل مشکل LQR
, ?LQR (?∗1, ?∗2, ?∗3, ?∗4)’s, ? = 1, 2, 3, 4
که در بالا تعریف شد، مشکل برنامه ریزی خطی (8) و (9) را نیز حل می کند.
اثبات:
از آنجایی که هم مشکل برنامهنویسی خطی و هم مشکل LQR راهحلهای ثابتی را فرض میکنند، هدف یافتن ?? های ثابت برای همه k است که به ترتیب مشکل برنامهنویسی خطی و مسئله LQR را همانطور که در جدول 1 نشان داده شده است، حل میکنند.
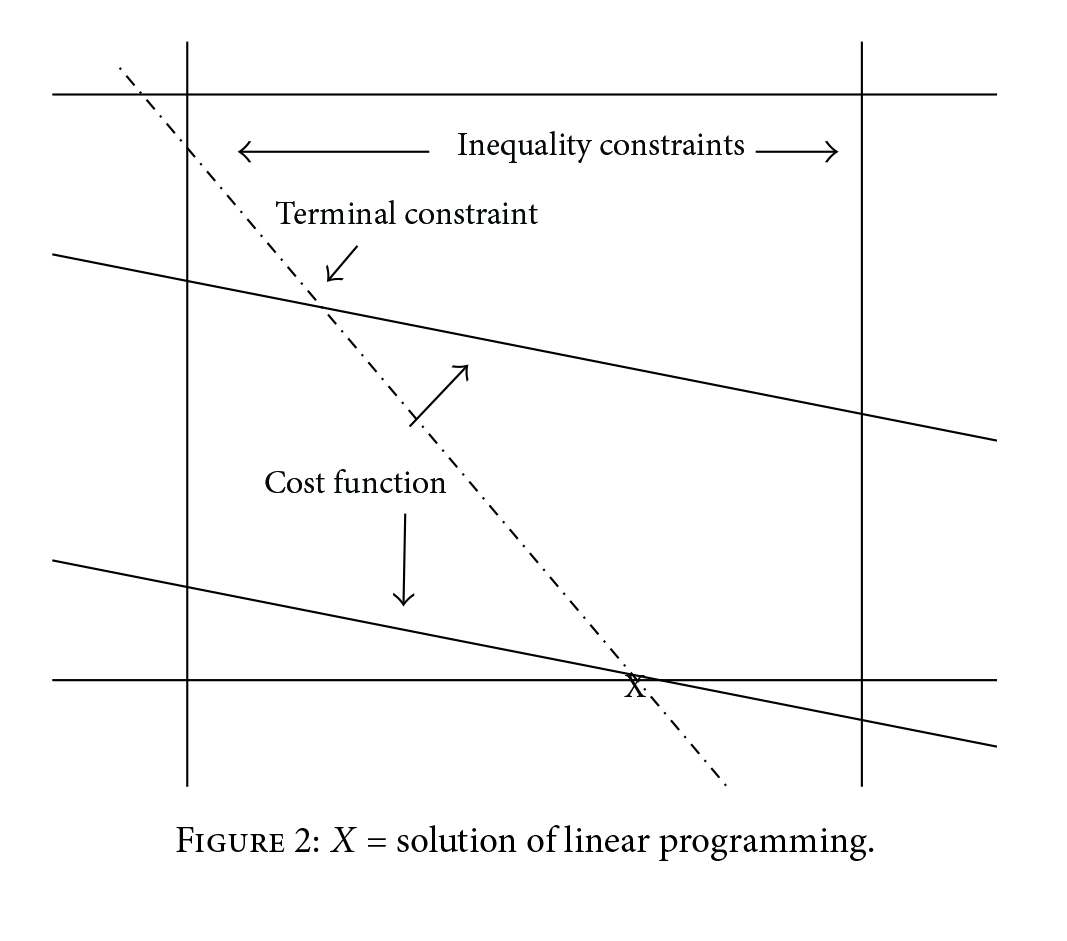
برای مشکل برنامهریزی خطی، حداقل یکی از راهحلهای بهینه در یکی از گوشههایی قرار دارد که توسط تقاطعهای ابرصفحههای تابع هزینه، محدودیت پایانه و محدودیتهای نابرابری همانطور که در شکل 2 برای حالت دو بعدی نشان داده شده است، قرار دارد. از طرف دیگر، راه حل مسئله LQR در تقاطع همان ابرصفحههایی است که توسط قیود پایانه و نابرابری و یک بیضی شکل میگیرند.
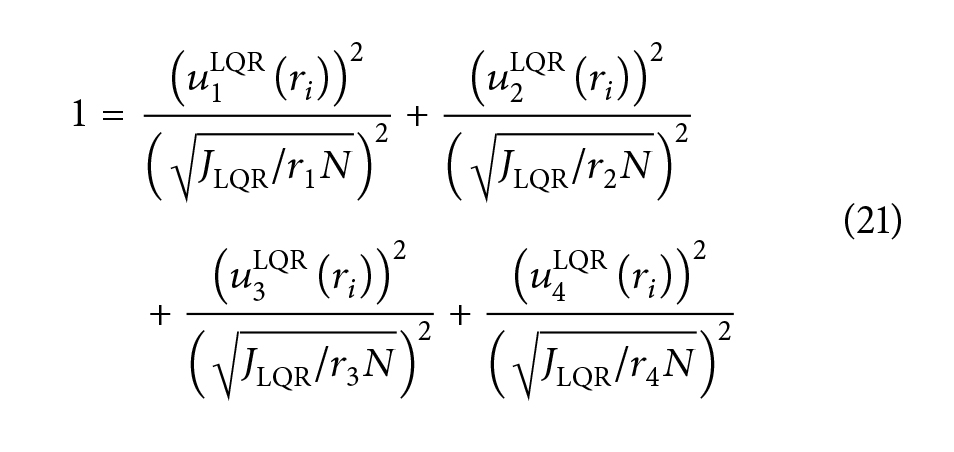
Journal of Energy
Journal of Energy
شکل 2: X راه حل برنامه ریزی خطی
برای یک مجموعه معین از ??. با تغییر ??، محورهای بیضی را میتوان به دلخواه تنظیم کرد و همیشه مقداری ?∗? وجود دارد به طوری که راه حل LQR در یکی از گوشهها قرار دارد و این راه حل مشکل برنامهریزی خطی را همانطور که در شکل 3 نشان داده شده است برای یک مورد دو بعدی حل میکتد. چنین راه حلهایی با معادله ?1LQR(??*), ?2LQR(??*), ?3LQR(?i*), ?4LQR(??*) نشان داده شده است.
این معادله نشان میدهد که:
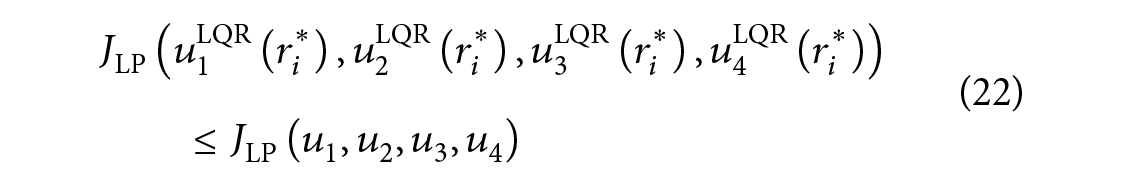
Journal of Energy
برای هر ?i یا تابع هزینه برنامهریزی خطی JLP که در راه حل LQR ارزیابی شده ?1LQR(??*), ?2LQR(??*), ?3LQR(?i*), ?4LQR(??*) نباید بزرگتر از (?LP(?1, ?2, ?3, ?4 برای هر ?i باشد.از طرف دیگر
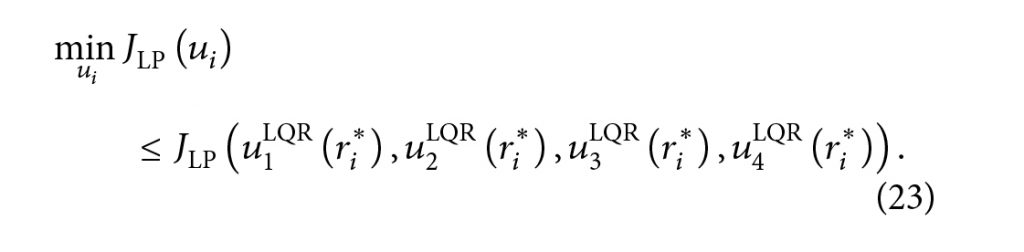
هزینه برنامه ریزی خطی
بنابراین راه حل ?1LQR(??*), ?2LQR(??*), ?3LQR(?i*), ?4LQR(??*) معادله LQR مشکل LP را نیز حل میکند. این اثبات را کامل میکند.
راه حل LQR
3.3 محاسبه و اعتبارسنجی ??* ها
آنچه نتایج قاعده 3 نشان می دهد این است که ثابتهای ui وجود دارد که مسائل LP و LQR را حل میکند. علاوه بر این اجازه دهید ?1(??), ?2(??), ?3(??), ?4(??) راه حل LQR برای ?1, ?2, ?3 و ?4 باشد. سپس
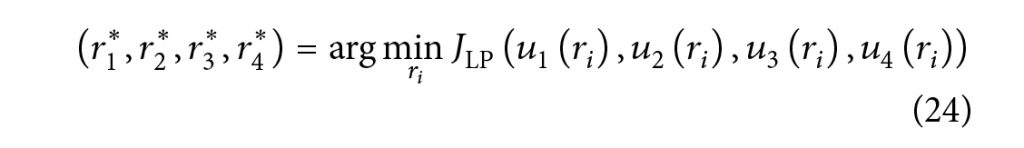
ثابتهای ui
و این راهی برای محاسبه ?i* فراهم میکند.
برای سادگی، اجازه دهید ابتدا تمام قیدهای نابرابری در (9) را کنار بگذاریم. قید نهایی و تابع هزینه را در نظر بگیرید،
برای یافتن راه حل lQR ما ضریب لانگراژ (Lagrange) را معرفی میکنیم.
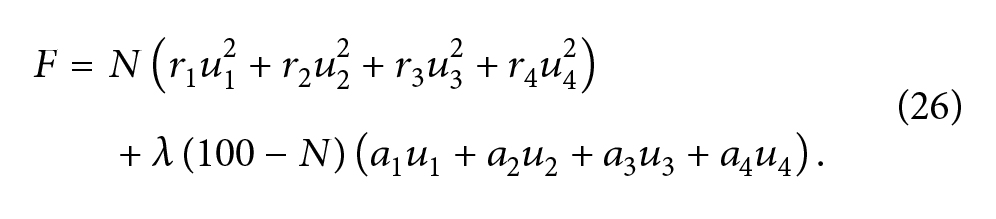
ضریب لانگراژ
قرار دادن مشتقات ? با توجه به ?1، ?2، ?3، ?4 و ? بر روی صفر به این معنی است که
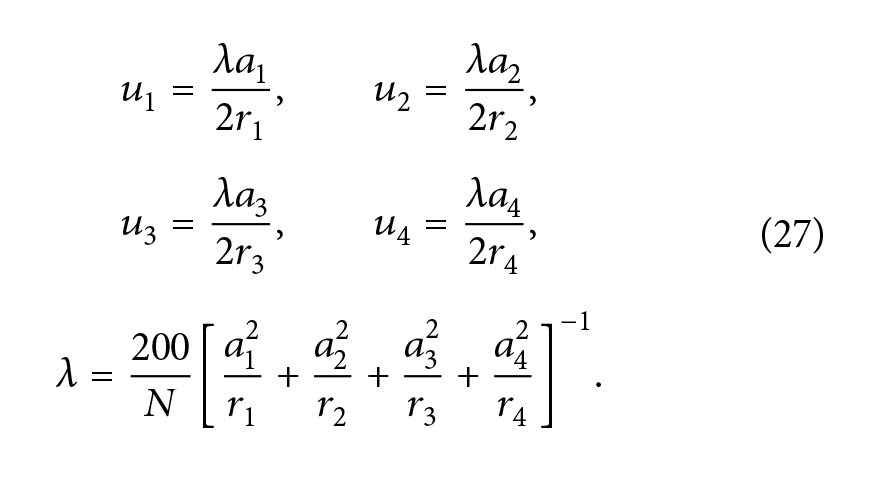
قرار دادن مشتقات
با حل این 5 معادله، ما داریم:

معادله
اکنون با برگرداندن این مقادیر به JLP داریم:
ما دو حالت داریم:
- اگر ?1, ?2, ?3, r4 ≥0 باشد، سپس دو مجموعه وزن (?1, ?2, ?3, r4) و (?1, ?2, ?3, r4) ? دنبالههای ورودی بهینه LQR یکسان را برای هر ?>0 تولید میکنند.
- در عمل، استفاده از انرژی الکتریکی همیشه مثبت است که به معنی ??*>0 است.
- بر اساس این دو حالت ممکن است ?1=1 تنظیم کنیم و
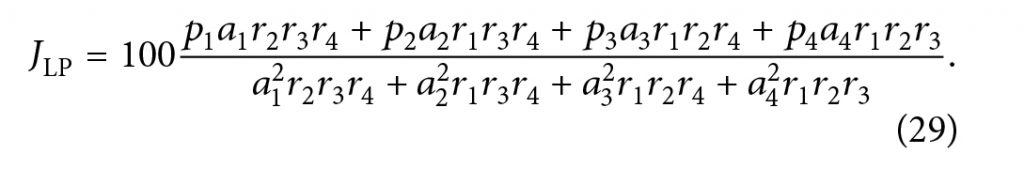
معادله
که به نوبه خود باعث معادله 31 میشود.
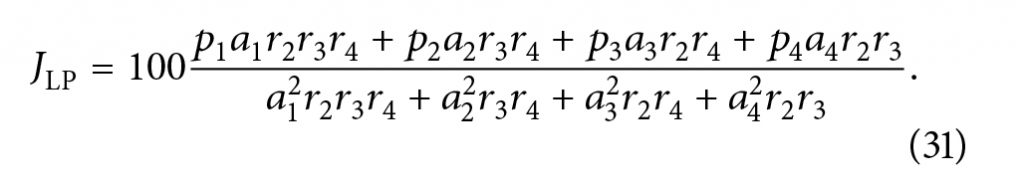
معادله
فرض کنید ??* مقدار ?LP بالا را به حداقل میرساند. سپس، ?? های بهینه آنهایی هستند که در (28) با جایگزین کردن ?? توسط ??* به دست آمد. اینها راه حلهای بدون قیدهای های نابرابری (9) هستند.
برای حمایت از مشتقات نظری فوق، تعداد زیادی از مجموعه دادههای تولید واقعی (بیش از 2 هزار) جمعآوری شده است. بر اساس 30 مجموعه داده که به طور تصادفی انتخاب شده، ابتدا مشکل برنامهریزی خطی (2) و (4) را مستقیماً با استفاده از دستور “linprog” تعبیه شده در MATLAB حل میکنیم. سپس همان مشکل را با یافتن ??* های بهینه و دنبالههای ورودی بهینه مربوطه ??*[?] ها از طریق بهینهسازی LQR همانطور که قبلا بحث شد حل میکنیم.
در هر مورد، نتایج بهینهسازی یکسان نیستند، اما تفاوت بسیار کمی در حدود 1-2٪ توابع هزینه دارند. ما معتقدیم که این تفاوت عددی کوچک 1-2٪ به دلیل نقص عددی MATLAB برای یک برنامهریزی خطی با ابعاد بزرگ است (8400 متغیر و 14000 قید).
4- تخمین پارامتر
در بخشهای قبلی، فرض میشود که ورودیهای ماتریس ? در دسترس باشند. در واقع، ? به فرآیند ذوب و به ویژه وزن قراضه بستگی دارد. به طور کلی، ورودیهای ? باید تخمین زده شوند. برای قرار دادن پارامترهای تخمین زده شد در یک دورنما، ابتدا فرآیند ذوب را شرح میدهیم. فرآیند ذوب یک فرآیند دستهای (بچ) است. یک بچ فولاد یک گرما نامیده میشود. زمان بین تپها مقدار زمان لازم برای تولید یک بچ فولاد مایع است.
مقدار فولاد تولیدی توسط وزن قراضه شارژ شده اندازه گیری میشود. ابتدا قراضه وارد کارخانه ذوب شده و با استفاده از جرثقیل سقفی به داخل سبدهای شارژ انتقال داده میشود. هنگامی که سبد شارژ بارگیری شد، جرثقیل سبد شارژ را برمیدارد و قراضه را در EAF قرار میدهد. EAF معمولاً با استفاده از فرآیند 3 شارژی کار میکند و یک چرخه ذوب از مراحل زیر تشکیل شده است.
1- بازرسی کوره – EAF بازرسی شده و برای گرمایش بعدی آماده میشود.
- شارژ – اولین قراضه در EAF قرار میگیرد.
- ذوب – جریان برق برقرار میشود و قراضه ذوب میشود تا زمانی که حجم به اندازه کافی کاهش یابد تا شارژ دوم در EAF قرار گیرد.
- چرخه شارژ و ذوب برای شارژهای دوم و سوم قراضه تکرار میشود.
- پالایش – آلیاژها در صورت لزوم به فولاد مایع اضافه میشوند و فولاد 100٪ ذوب میشود.
- تپ – فولاد مایع از EAF به یک پاتیل برای ریختهگری منتقل میشود.بدیهی است که بسته به وزن قراضه در سه شارژ، مقادیر ورودی ? متفاوت است. برای این منظور، ما یک شناسه، l = کم، m = متوسط، و h = زیاد برای هر بار شارژ ارائه میکنیم تا میزان قراضه بارگیری شده در هر شارژ را منعکس کند. بنابراین، همانطور که در جدول 2 نشان داده شده است، در مجموع 9 سناریو مختلف بارگیری قراضه وجود دارد. برای مثال، اگر سه بار شارژ برای یک گرمایش خاص (یک ذوب مشخص) به ترتیب 32 تن (شارژ اول)، 32 تن (شارژ دوم) و 18 تن (شارژ سوم) باشد و به صورت (1l,2l,3l) مشخص میشود.
اگر سه مرحله شارژ به ترتیب 32 تن، 34 تن و 23 تن باشد، به صورت (1l,2m,3h). مشخص میشود. برای هر سناریو، ورودی های ? به طور جداگانه تخمین زده میشود. برای برآورد واقعی، اجازه دهید
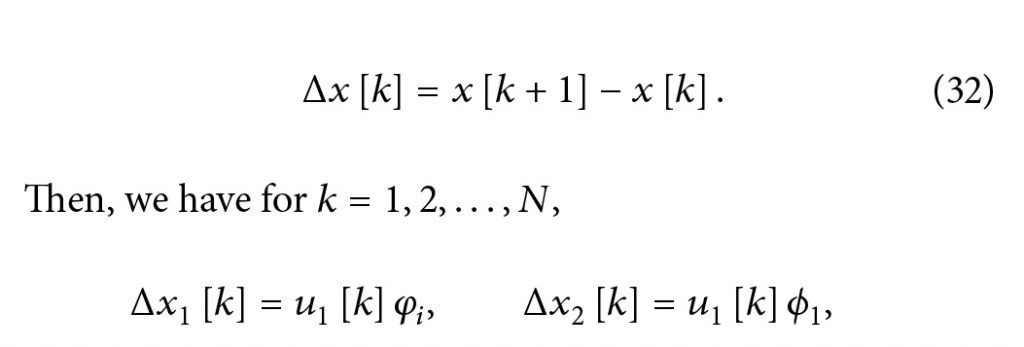
Journal of Energy
سپس برای k=1, 2, ….., N داریم:
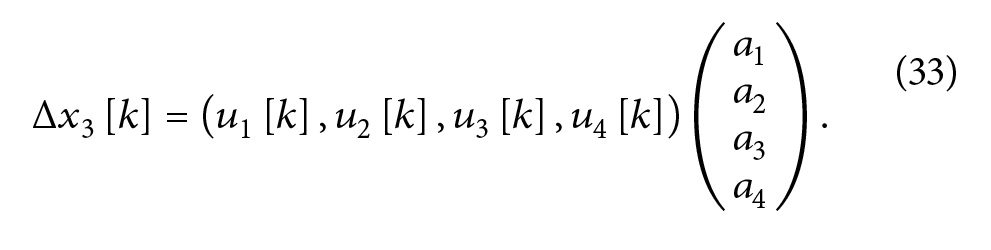
Journal of Energy
Journal of Energy
-

Journal of Energy
می توان به صورت زیر به راحتی حل کرد:
-
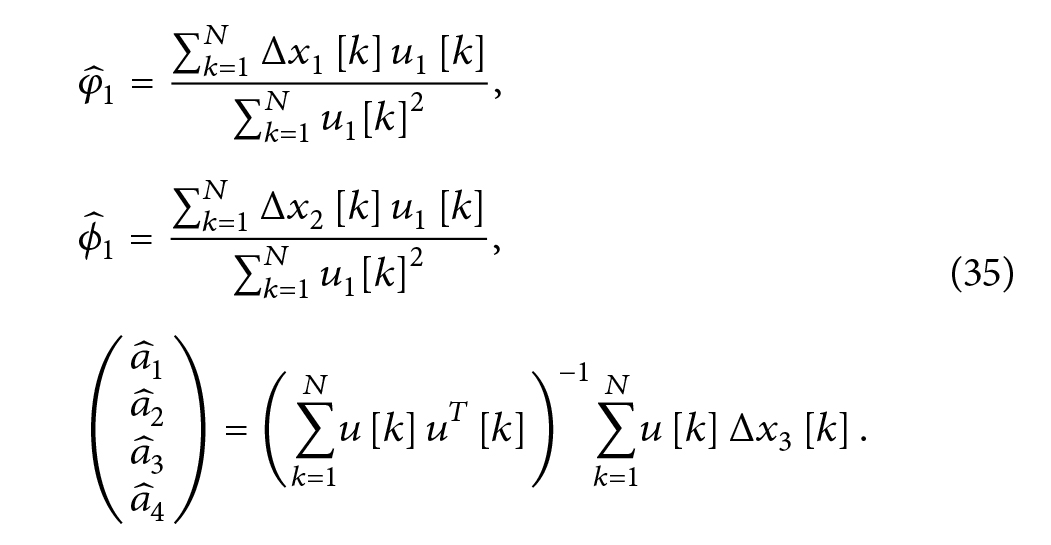
Journal of Energy
برای تایید نتایج پارامتر تخمین زده شده، اجازه می دهیم که:
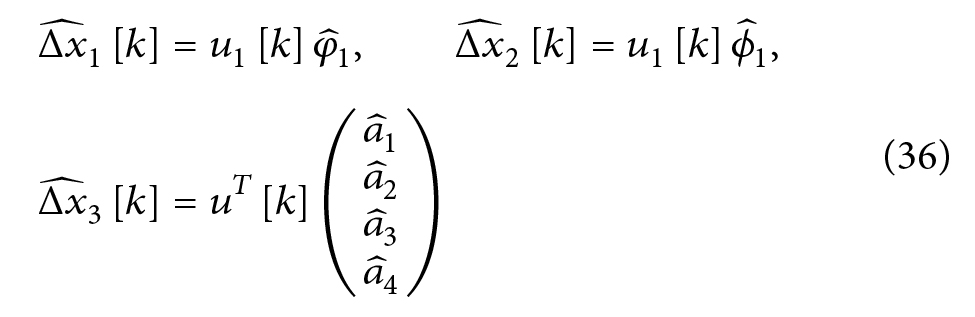
Journal of Energy
-
و Goodness-of Fit را به این صورت تعریف کنید:
-
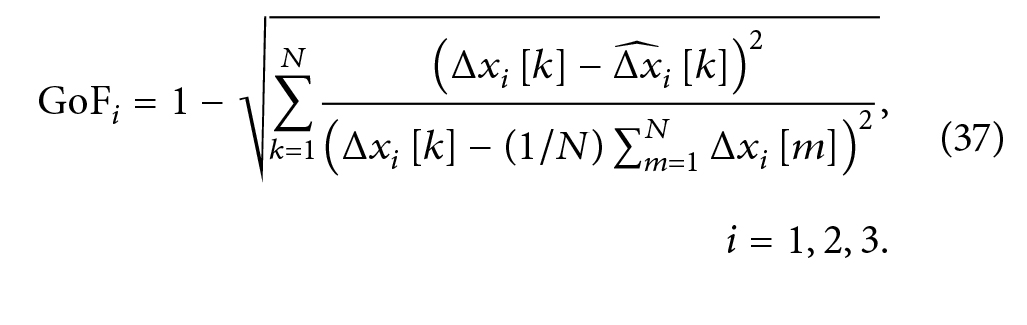
Journal of Energy
Journal of Energy
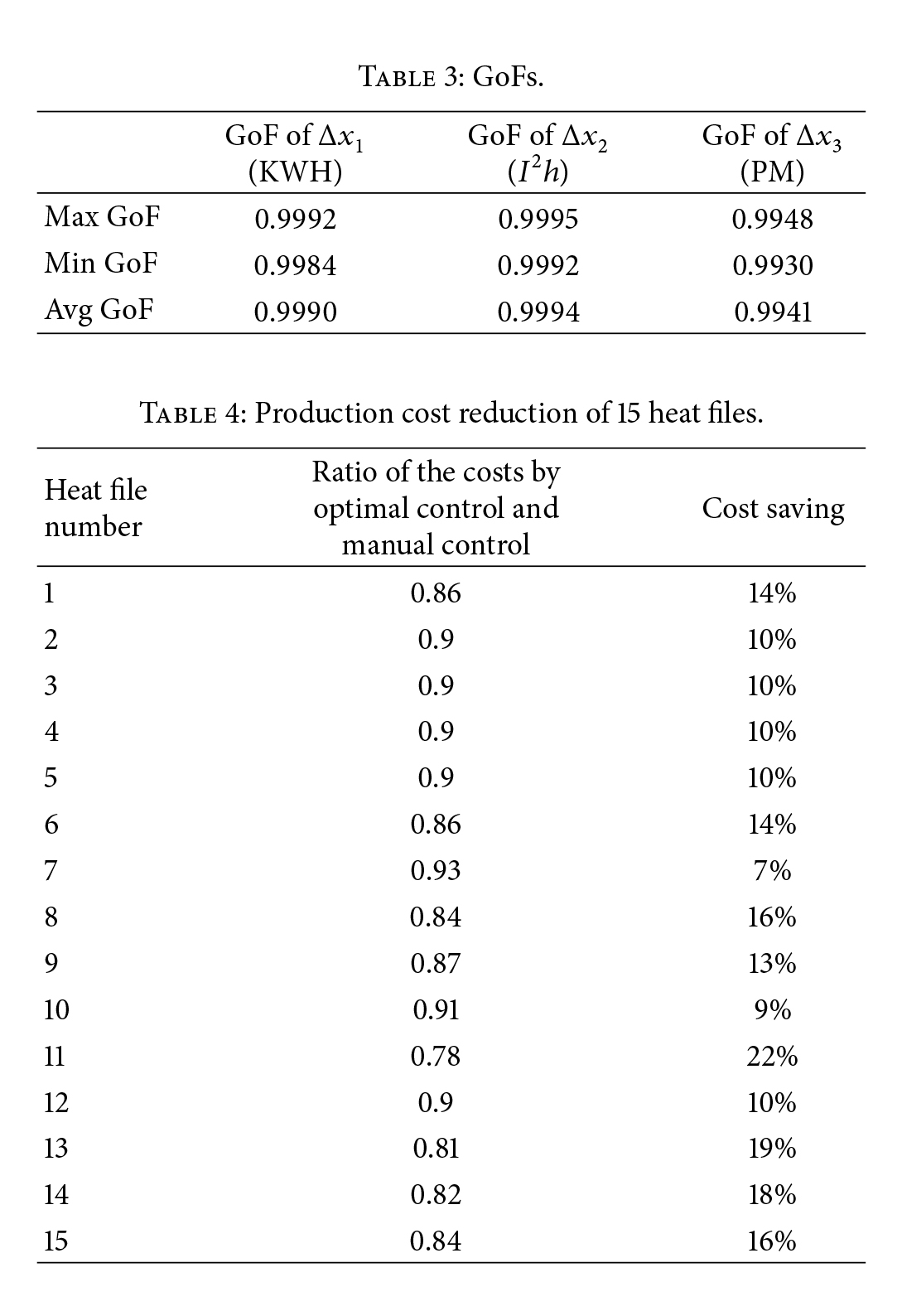
پارامترها از یک فایل گرمایشی مشتق شدهاند و توسط 30 فایل گرمایش تازه دیگر که برای تخمین استفاده نشدهاند، اما با همان شناسه استفاده شدهاند، اعتبارسنجی شدهاند. نتایج اعتبارسنجی در جدول 3 نشان داده شده است. از جدول 3 واضح است که نتایج رضایت بخش است و مقادیر در و طرح کنترلی برای جایگزینی مجهولات و ?? ها استفاده خواهد شد.
5- اعتبار سنجی طرح کنترلی
همانطور که قبلاً گفته شد، طرح کنترلی شامل دو مرحله است:
- ورودیهای ? را برای وزن های بار قراضه مختلف تخمین بزنید.
- بر اساس تخمینها، ?? بهینه را برای مسئله LQR و ورودیهای بهینه مربوطه ?* (?∗1, ?∗2, ?∗3, ?∗4).
به یاد بیاورید که هدف ما طراحی توالیهای ورودی بهینه است به طوری که هزینه تولید (2) در مقایسه با عملیات دستی فعلی که تجربیات نقش کلیدی در آن دارند، به حداقل برسد. در این فرضیه، نشان داده شده است که راه حل LQR (?* (?∗1, ?∗2, ?∗3, ?∗4)’s, ? = 1, 2, 3, 4,) مشکل LP را نیز حل میکند و به سبب آن هزینه تولید (2) را تحت قیدها به حداقل میرساند. اینکه آیا در واقعیت کار میکند یا خیر، باید تأیید شود. برای این منظور، ما به طور تصادفی 15 فایل گرمایش واقعی را با هزینههای تولید مشخص انتخاب میکنیم. برای هر فایل گرمایشی، یک فایل گرمایشی تازه با همان شناسه اما نه شناسهای که در 15 فایل اصلی انتخاب شده و برای تخمین ورودیهای ? برای ساخت مدل EAF و محاسبه راه حلهای LQR بهینه ?* (?∗1, ?∗2, ?∗3, ?∗4)’s, ? = 1, 2, 3, 4 استفاده میشود. ورودیهای بهینه به فایل اصلی برمیگردند تا هزینه تولید را با طرح کنترلی بهینه محاسبه کنند. بر اساس هزینه تولید اصلی (2)، نسبتهای هزینهها توسط طرحهای کنترلی بهینه به دست آمده توسط LQR که در آن وزنهای ?? ها برای به حداقل رساندن هزینه LP تنظیم میشوند و با روش دستی فعلی همراه با درصد صرفهجویی در هزینه در جدول 4 نشان داده شده است. در تمام 15 آزمایش (فایل)، ورودیهای بهینه محدودیتها (9) را برآورده میکند و هزینه تولید را از 7٪ تا 22٪ کاهش میدهد. این از مشتق تئوری ما پشتیبانی میکند و نشان میدهد که هزینه تولید که در آن مصرف انرژی بخش اصلی است، میتواند با تغییر روش از حالت دستی به خودکار به طور قابل ملاحظهای کاهش یابد.
- نتیجهگیری و کار آینده
روش پیشنهادی برای استراتژی کنترل بهینه یک کوره قوس، یک طرح قوی حلقه بسته ارائه میکند که هزینه تولید فولاد EAF را بهینه میکند. در این مطالعه، ما بر روی 7 متغیر کلیدی و یک مدلسازی خطی تمرکز میکنیم. در آینده، سایر متغیرهای جزئی و احتمالاً اثرات غیرخطی را میتوان و باید در نظر گرفت. انتظار میرود با ترکیب همه عوامل، هزینه تولید کاهش بیشتری یابد. همچنین، استراتژی توسعهیافته در این مقاله را میتوان به برنامههای کاربردی دیگری که در آن تابع هزینه خطی و طرح کنترلی استفاده شده درجه دوم است، تعمیم داد.
تعارض به منافع:
نویسنده اعلام میکند که در مورد انتشار این مقاله تعارض به منافع وجود ندارد.
سپاسگزاری:
این کار توسط گرنت مرکز انرژی آیووا 01-09 پشتیبانی شد.
منابع:
[1] R. Balan, V.Maties, O. Hancu, S. Stan, and L. Ciprian, “Modeling and control of an electric arc furnace,” in Proceedings of the 15Mediterranean Conference on Control and Automation, pp. 1– 6, Athens, Greece, July 2007.
[2] B. Boulet, G. Lalli, and M. Ajersch, “Modeling and control of an electric arc furnace,” in Proceedings of the American Control
Conference, pp. 3060–3064, Denver, Colo, USA, June 2003.
[3] ¨ U. C¸ amdali and M. Tunc¸, “Modelling of electric energy consumption in the AC electric arc furnace,” International Journal
of Energy Research, vol. 26, no. 10, pp. 935–947, 2002.
[4] Anuradha, K. B. Muni, and A. Kumar, “Modeling of EFA and control algorithms for voltage flicker mitigation using
DSTATCOM,” in Proceedings of the 16th National Power Systems Conference, Hyderabad, India, December 2010.
